Capítulo 28 Suavización

Antes de continuar aprendiendo sobre algoritmos de machine learning, presentamos el importante concepto de suavización (smoothing en inglés). La suavización es una técnica muy poderosa comúnmente usada en el análisis de datos. Otros nombres dados a esta técnica son ajustamiento de curvas y filtro de paso bajo (curve fitting y low pass filtering en inglés). La suavización está diseñada para detectar tendencias en presencia de datos ruidosos cuando se desconoce la forma real de la tendencia. El nombre suavización proviene del hecho de que para lograr esta hazaña, suponemos que la tendencia es suave, como una superficie lisa. En cambio, el ruido (noise en inglés), o la desviación de la tendencia, es impredeciblemente ondulante:

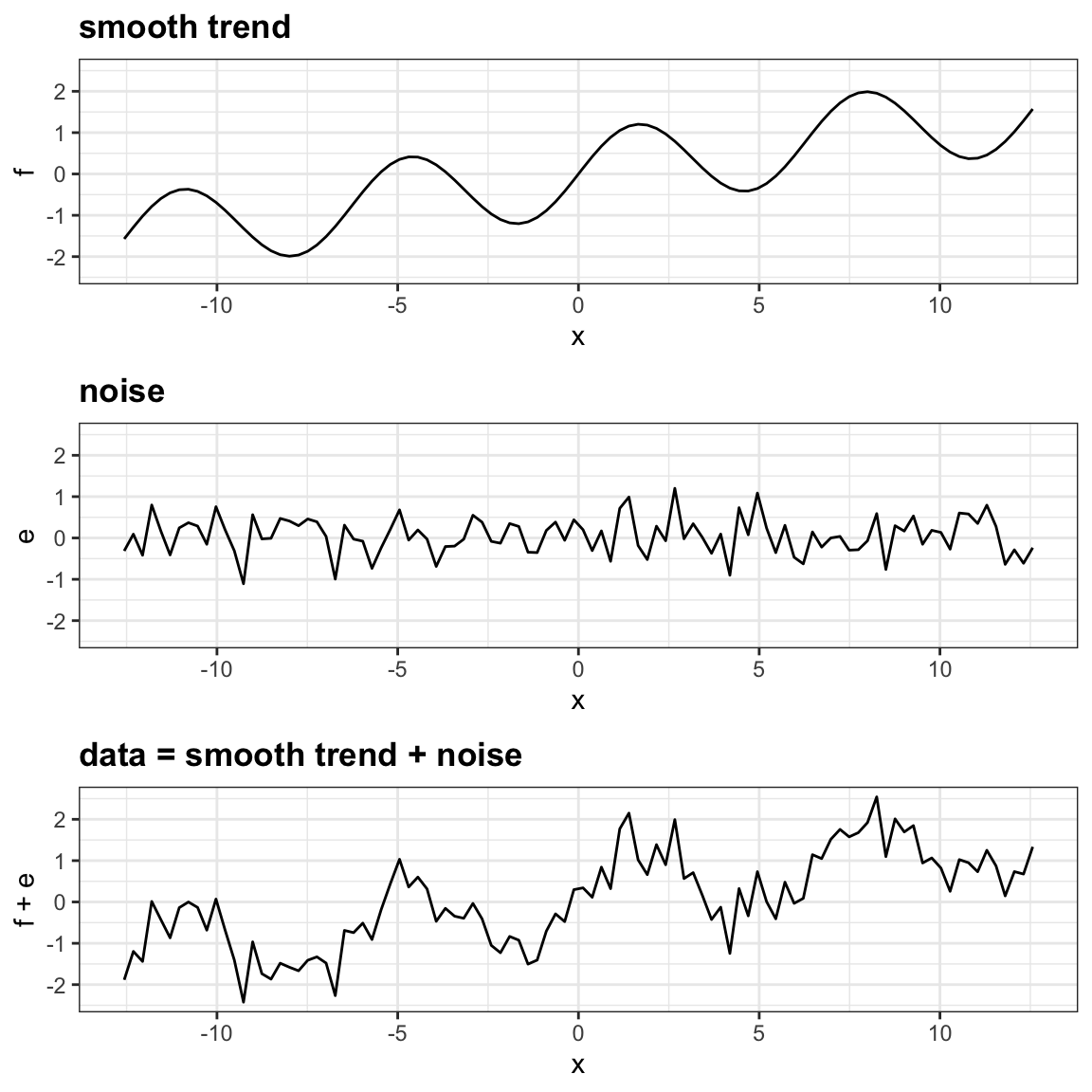
Parte de lo que explicamos en esta sección son los supuestos que nos permiten extraer la tendencia del ruido.

Para entender por qué cubrimos este tema, recuerden que los conceptos detrás de las técnicas de suavización son extremadamente útiles en machine learning porque las expectativas/probabilidades condicionales que necesitamos estimar pueden considerarse como tendencias de formas desconocidas afectadas por incertidumbre.

Para explicar estos conceptos, nos enfocaremos primero en un problema con un solo predictor. Específicamente, tratamos de estimar la tendencia temporal en el margen de la encuesta de votación popular de 2008 en Estados Unidos (la diferencia entre Obama y McCain).

library(tidyverse)
library(dslabs)
data("polls_2008")
qplot(day, margin, data = polls_2008)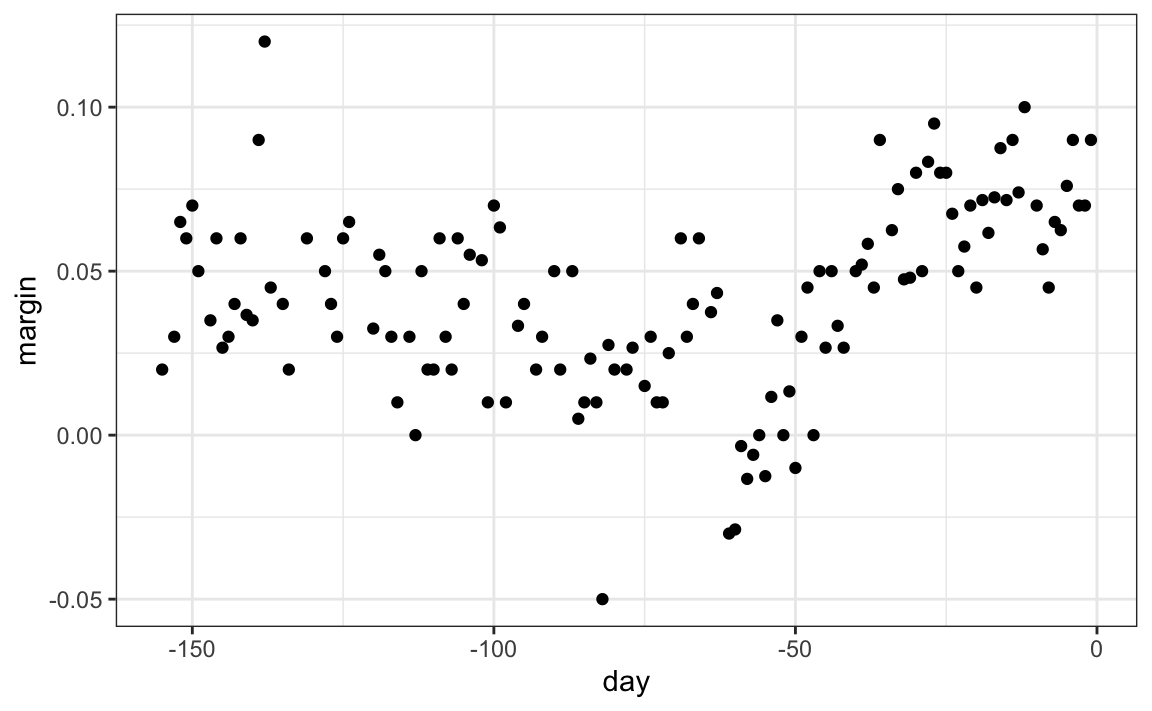

Para los fines de este ejemplo, no lo piensen como un problema de pronóstico. En cambio, simplemente estamos interesados en entender la forma de la tendencia después de que terminen las elecciones.

Suponemos que para cualquier día \(x\), hay una verdadera preferencia entre el electorado \(f(x)\), pero debido a la incertidumbre introducida por el sondeo, cada punto de datos viene con un error \(\varepsilon\). Un modelo matemático para el margen de encuesta observado \(Y_i\) es:

\[ Y_i = f(x_i) + \varepsilon_i \]

Para pensar en esto como un problema de machine learning, recuerden que queremos predecir \(Y\) dado un día \(x\). Si supiéramos la expectativa condicional \(f(x) = \mbox{E}(Y \mid X=x)\), la usaríamos. Pero como no conocemos esta expectativa condicional, tenemos que estimarla. Usemos la regresión, ya que es el único método que hemos aprendido hasta ahora.

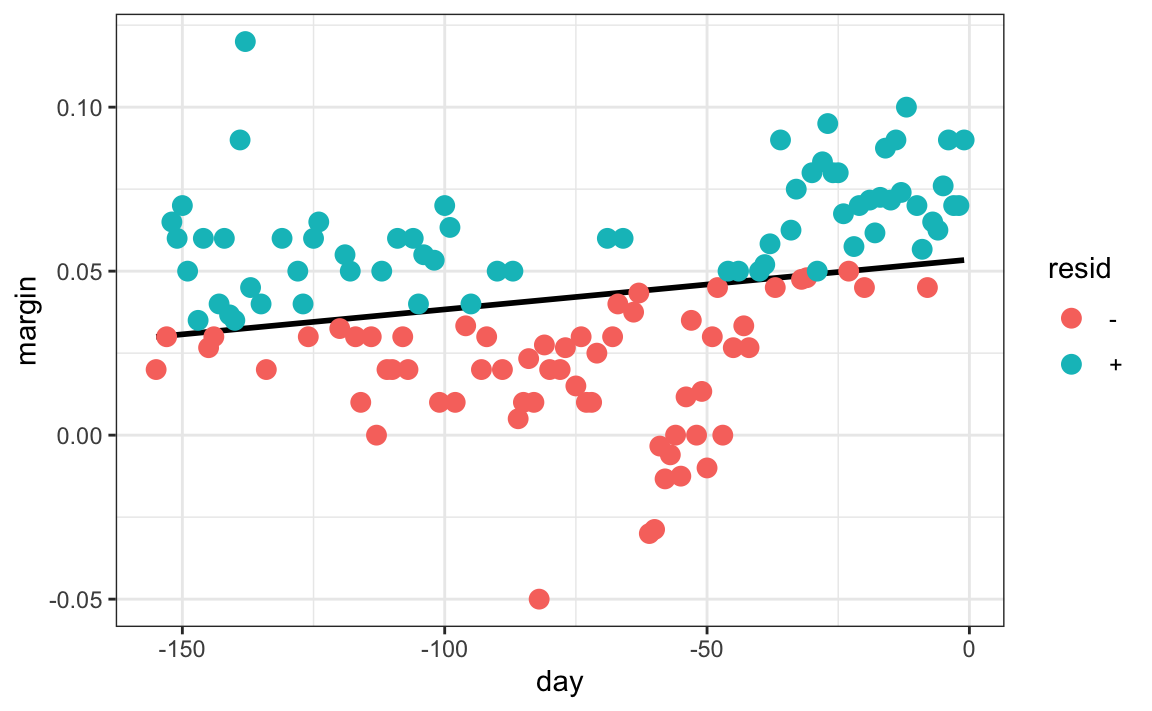
La línea que vemos no parece describir muy bien la tendencia. Por ejemplo, el 4 de septiembre (día -62), se celebró la Convención Republicana y los datos sugieren que este evento le dio a John McCain un impulso en las encuestas. Sin embargo, la línea de regresión no captura esta tendencia potencial. Para ver más claramente la falta de ajuste, observamos que los puntos por encima de la línea ajustada (azul) y los de abajo (rojo) no se distribuyen uniformemente entre los días. Por lo tanto, necesitamos un enfoque alternativo más flexible.

28.1 Suavización de compartimientos

La idea general de la suavización es agrupar los puntos de datos en estratos en los que el valor de \(f(x)\) se puede suponer que es constante. Podemos hacer esta suposición porque pensamos que \(f(x)\) cambia lentamente y, como resultado, \(f(x)\) es casi constante en pequeñas ventanas de tiempo. Un ejemplo de esta idea para los datos poll_2008 es suponer que la opinión pública se mantuvo aproximadamente igual en el plazo de una semana. Con este supuesto, tenemos varios puntos de datos con el mismo valor esperado.

Si fijamos un día para estar en el centro de nuestra semana, llámelo \(x_0\), entonces para cualquier otro día \(x\) tal que \(|x - x_0| \leq 3.5\), suponemos que \(f(x)\) es una constante \(f(x) = \mu\). Esta suposición implica que: \[ E[Y_i | X_i = x_i ] \approx \mu \mbox{ if } |x_i - x_0| \leq 3.5 \]

En la suavización, llamamos el tamaño del intervalo que satisface \(|x_i - x_0| \leq 3.5\), el tamaño de la ventana, parámetro de suavizado o span. Más adelante, aprenderemos como intentamos optimizar este parámetro.

Esta suposición implica que un buen estimador de \(f(x)\) es el promedio de \(Y_i\) valores en la ventana. Si definimos \(A_0\) como el conjunto de índices \(i\) tal que \(|x_i - x_0| \leq 3.5\) y \(N_0\) como el número de índices en \(A_0\), entonces nuestro estimador es:

\[ \hat{f}(x_0) = \frac{1}{N_0} \sum_{i \in A_0} Y_i \]

La idea detrás de la suavización de compartimientos (bin smoothing en inglés) es hacer este cálculo con cada valor de \(x\) como el centro. En el ejemplo de la encuesta, para cada día, calcularíamos el promedio de los valores dentro de una semana con ese día en el centro. Aquí hay dos ejemplos: \(x_0 = -125\) y \(x_0 = -55\). El segmento azul representa el promedio resultante.

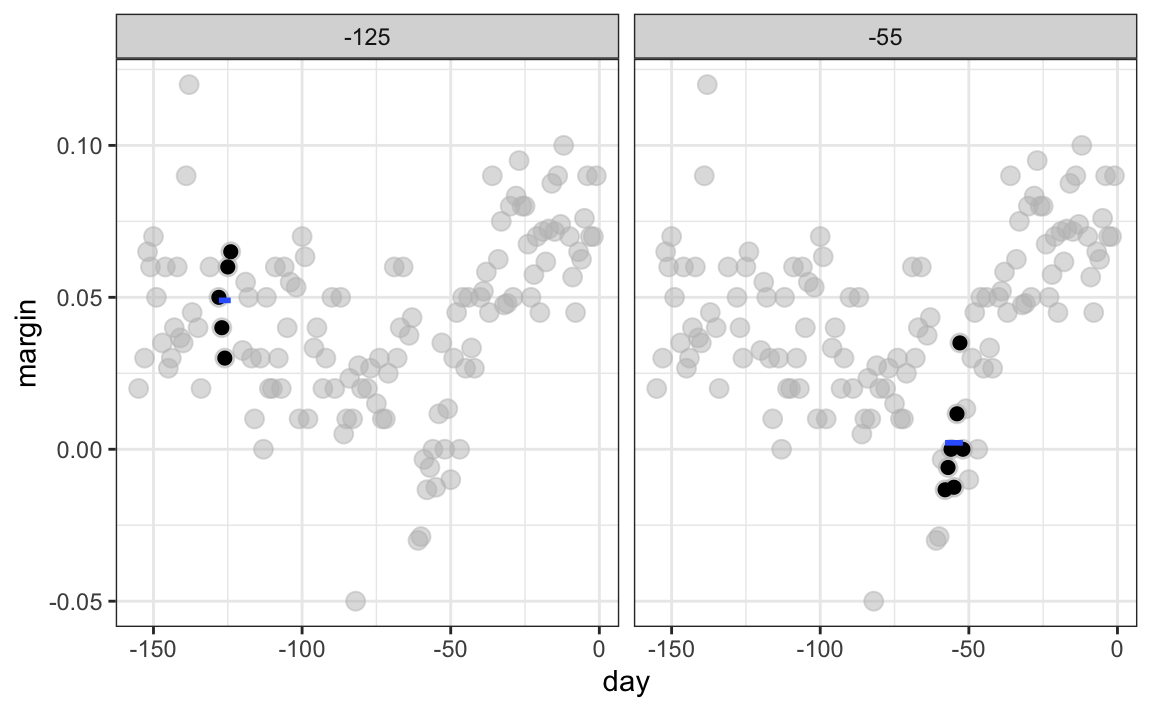
Al calcular esta media para cada punto, formamos un estimador de la curva subyacente \(f(x)\). A continuación, mostramos el procedimiento que ocurre a medida que avanzamos de -155 a 0. En cada valor de \(x_0\), mantenemos el estimador \(\hat{f}(x_0)\) y continuamos al siguiente punto:

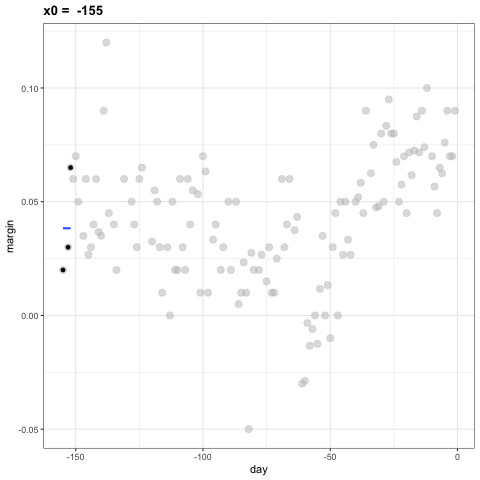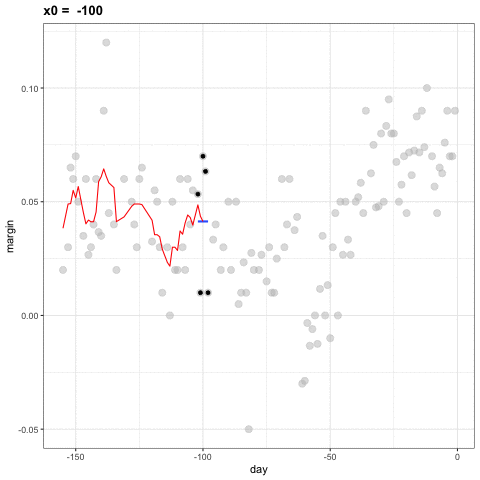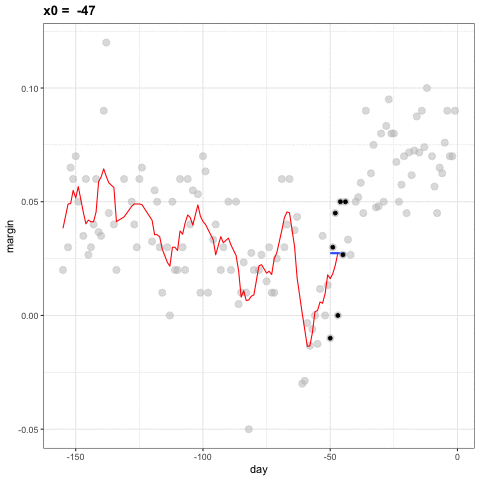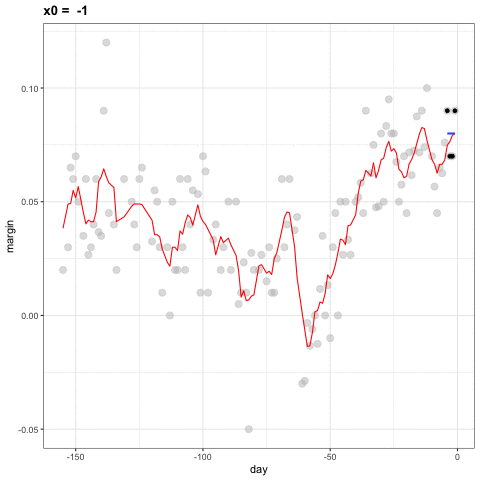
El código final y el estimador resultante se ven así:

span <- 7
fit <- with(polls_2008,
            ksmooth(day, margin, kernel = "box", bandwidth = span))

polls_2008 |> mutate(smooth = fit$y) |>
  ggplot(aes(day, margin)) +
  geom_point(size = 3, alpha = .5, color = "grey") +
  geom_line(aes(day, smooth), color="red")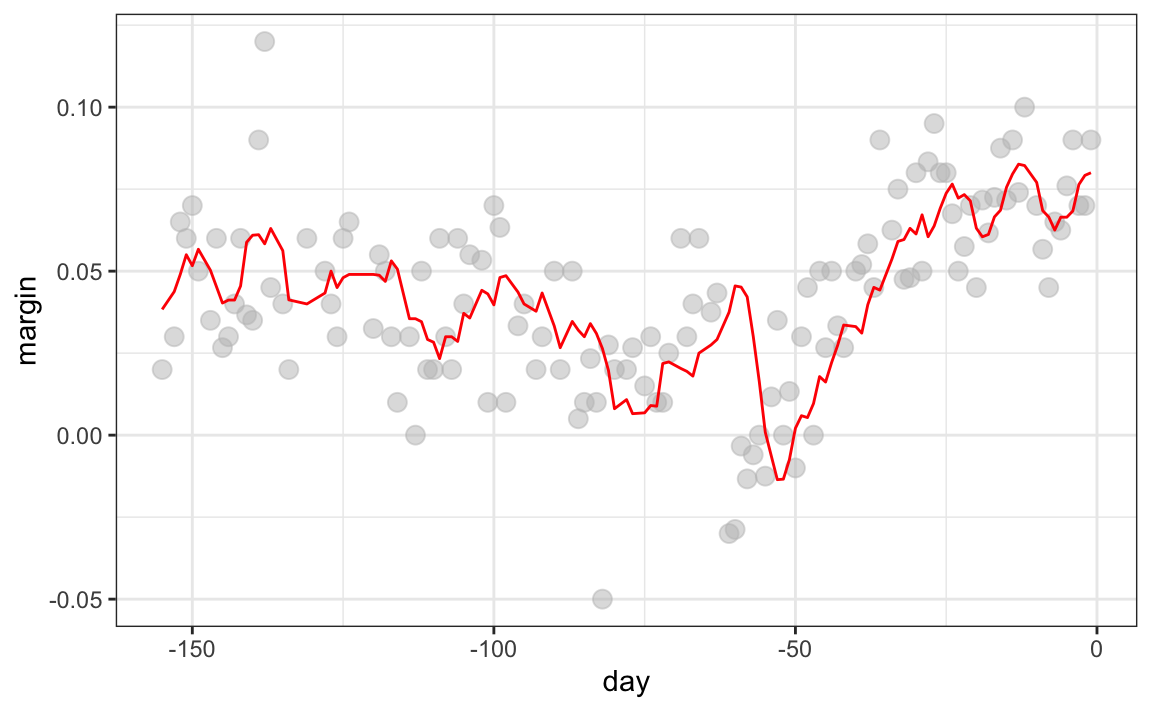

28.2 Kernels

El resultado final de la suavización de compartimientos es bastante ondulante. Una de las razones es que cada vez que la ventana se mueve, cambian dos puntos. Podemos atenuar esto algo tomando promedios ponderados que le dan al punto central más peso que a los puntos lejanos, con los dos puntos en los bordes recibiendo muy poco peso.

Pueden pensar en el enfoque de suavización de compartimiento como un promedio ponderado:

\[ \hat{f}(x_0) = \sum_{i=1}^N w_0(x_i) Y_i \]

en el que cada punto recibe un peso de \(0\) o \(1/N_0\), con \(N_0\) el número de puntos en la semana. En el código anterior, usamos el argumento kernel="box" en nuestra llamada a la función ksmooth. Esto se debe a que la función de peso \(w_0(x)\) parece una caja. La función ksmooth ofrece una opción “más suave” que utiliza la densidad normal para asignar pesos.

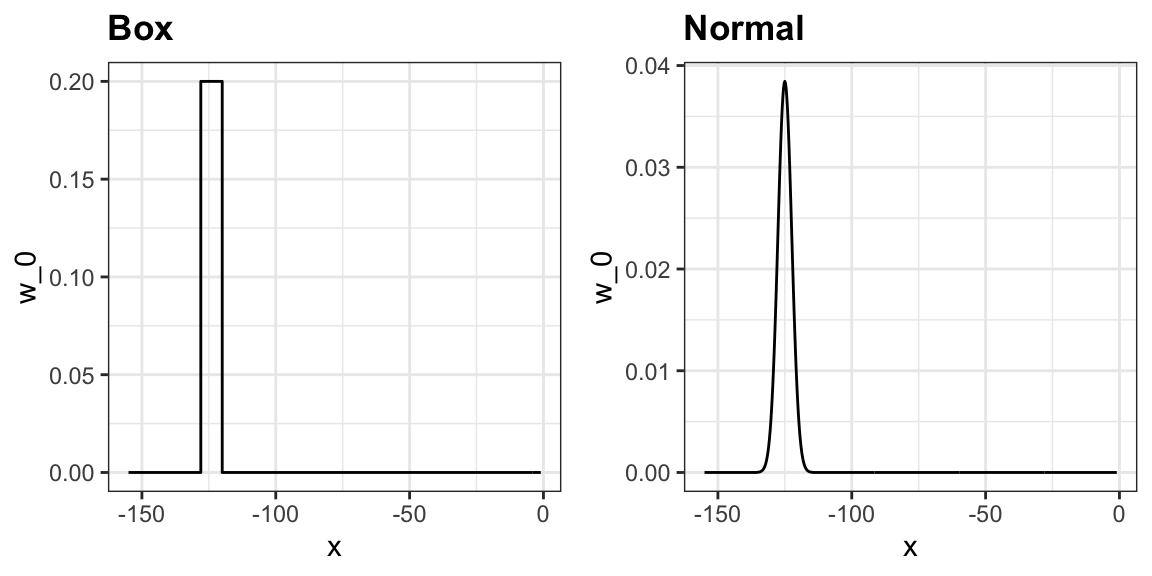
El código final y el gráfico resultante para el kernel normal se ven así:

span <- 7
fit <- with(polls_2008,
            ksmooth(day, margin, kernel = "normal", bandwidth = span))

polls_2008 |> mutate(smooth = fit$y) |>
  ggplot(aes(day, margin)) +
  geom_point(size = 3, alpha = .5, color = "grey") +
  geom_line(aes(day, smooth), color="red")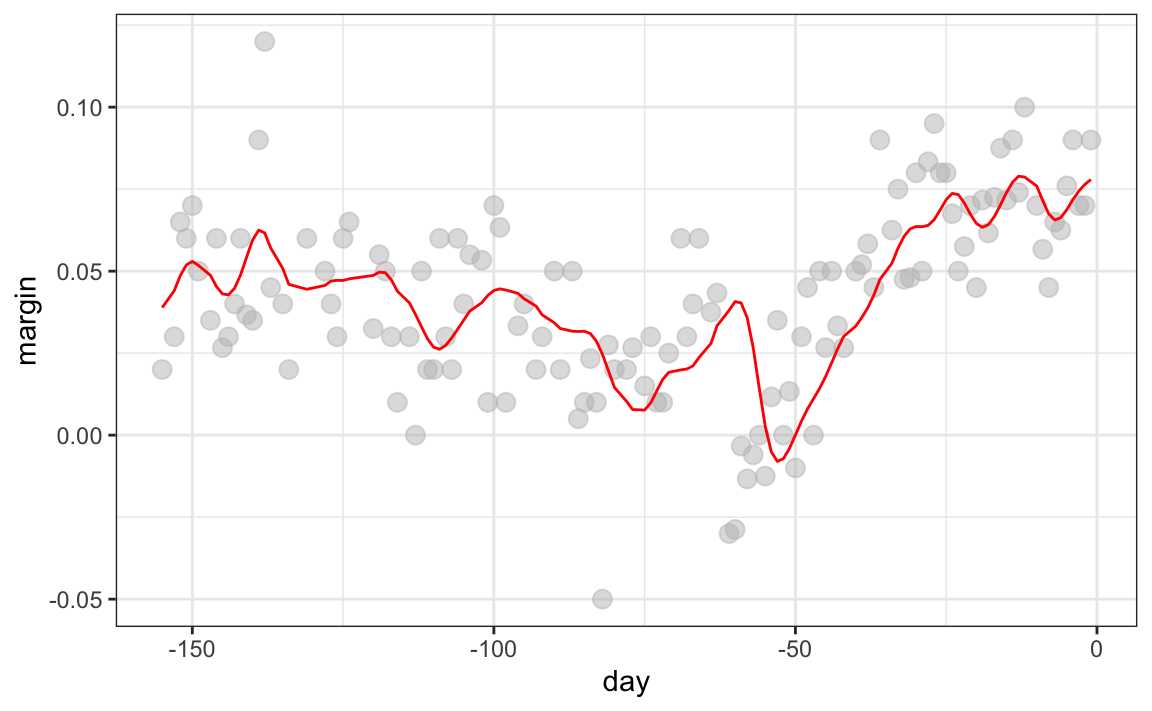

Observen que el estimador final ahora se ve más suave.

Hay varias funciones en R que implementan suavizadores de compartimientos. Un ejemplo es ksmooth, que mostramos arriba. En la práctica, sin embargo, generalmente preferimos métodos que usan modelos ligeramente más complejos que ajustar una constante. El resultado final arriba, por ejemplo, todavía es algo ondulante en partes que no esperamos que sea (entre -125 y -75, por ejemplo). Métodos como loess, que explicamos a continuación, mejoran esto.

28.3 Regresión ponderada local (loess)

Una limitación del enfoque de suavización de compartimientos que acabamos de describir es que necesitamos ventanas pequeñas para que se cumpla el supuesto de que la función es aproximadamente constante. Como resultado, terminamos con un pequeño número de puntos de datos para promediar y obtener estimaciones imprecisas \(\hat{f}(x)\). Aquí describimos cómo la regresión ponderada local (loess o local weighted regression en inglés) nos permite considerar tamaños de ventana más grandes. Para hacer esto, usaremos un resultado matemático, conocido como el teorema de Taylor, que dice que si examinamos muy de cerca cualquier función suave \(f(x)\), parecerá una línea. Para ver por qué esto tiene sentido, consideren los bordes curvos que hacen los jardineros con palas rectas:

(“Downing Street garden path edge”¹⁰⁷ del usuario de Flckr Número 10¹⁰⁸. Licencia CC-BY 2.0¹⁰⁹.)

En lugar de suponer que la función es aproximadamente constante en una ventana, suponemos que la función es localmente lineal. Podemos considerar tamaños de ventana más grandes cuando suponemos que la función es localmente lineal que cuando suponemos que es localmente constante. En lugar de la ventana de una semana, consideramos una ventana más grande en la que la tendencia es aproximadamente lineal. Comenzamos con una ventana de tres semanas y luego consideramos y evaluamos otras opciones:

\[ E[Y_i | X_i = x_i ] = \beta_0 + \beta_1 (x_i-x_0) \mbox{ if } |x_i - x_0| \leq 21 \]

Para cada punto \(x_0\), loess define una ventana y ajusta una línea dentro de esa ventana. Aquí hay un ejemplo que muestra los ajustes para \(x_0=-125\) y \(x_0 = -55\):

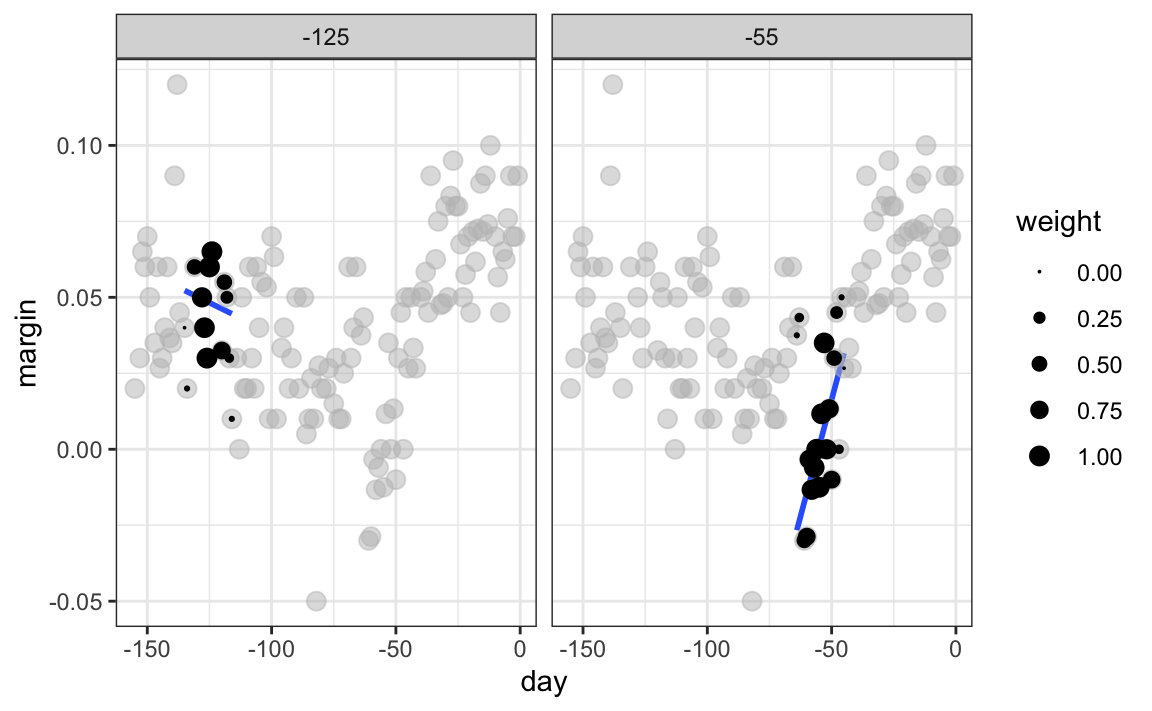
El valor ajustado en \(x_0\) se convierte en nuestro estimador \(\hat{f}(x_0)\). A continuación, mostramos el procedimiento que ocurre mientras cambiamos de -155 a 0.

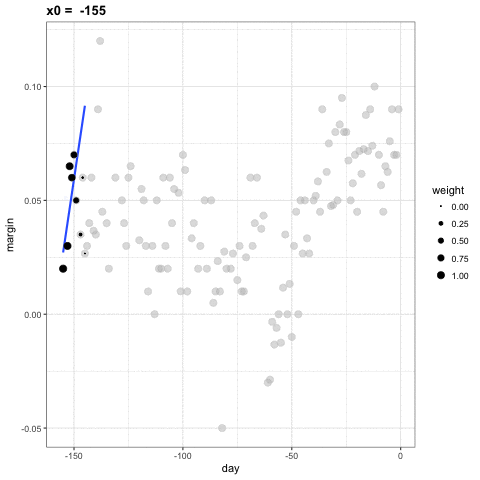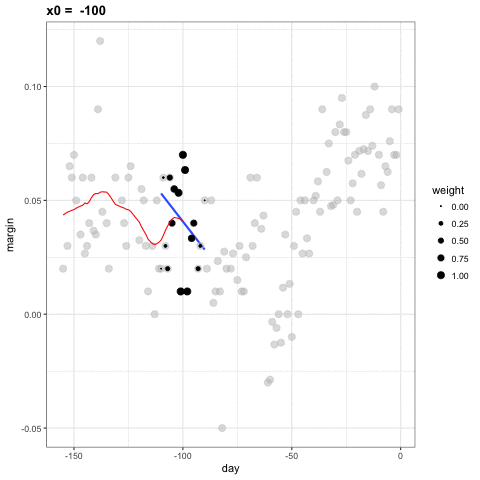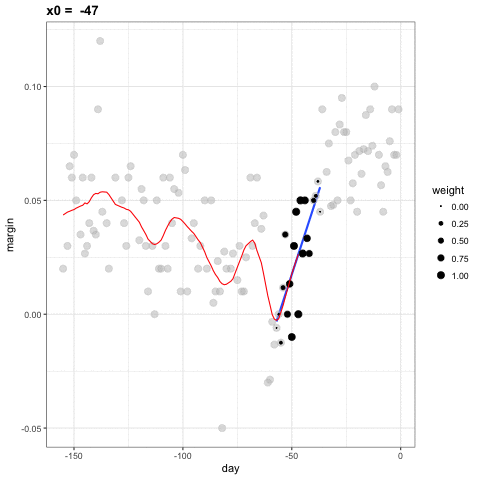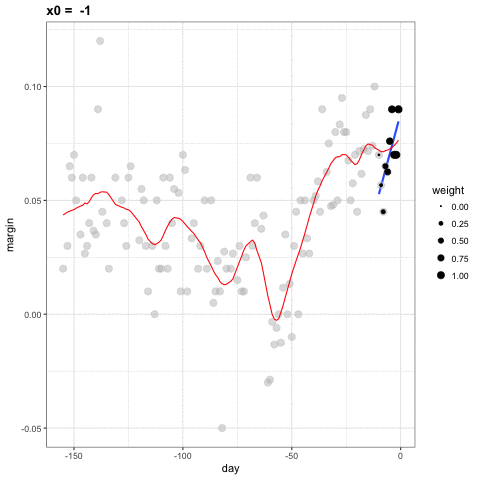
El resultado final es un ajuste más suave que ese producido por la suavización de compartimiento porque utilizamos tamaños de muestra más grandes para estimar nuestros parámetros locales:

total_days <- diff(range(polls_2008$day))
span <- 21/total_days

fit <- loess(margin ~ day, degree=1, span = span, data=polls_2008)

polls_2008 |> mutate(smooth = fit$fitted) |>
  ggplot(aes(day, margin)) +
  geom_point(size = 3, alpha = .5, color = "grey") +
  geom_line(aes(day, smooth), color="red")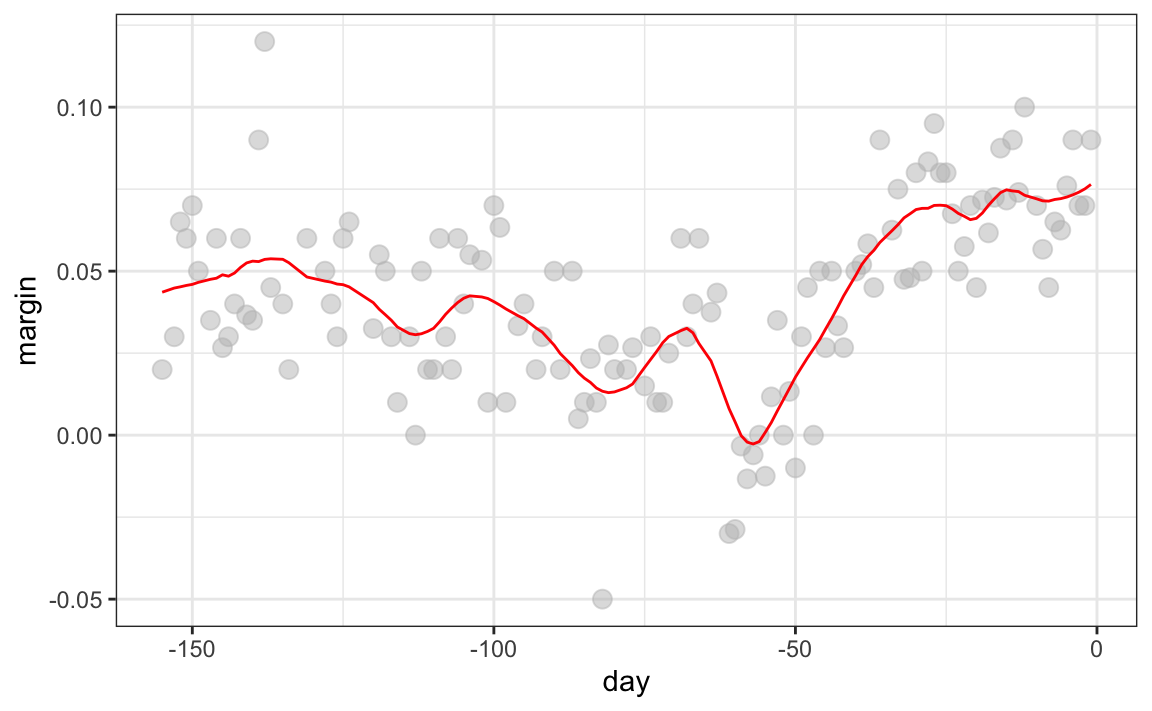

Podemos ver cómo diferentes tamaños de ventanas, spans, conducen a diferentes estimadores:

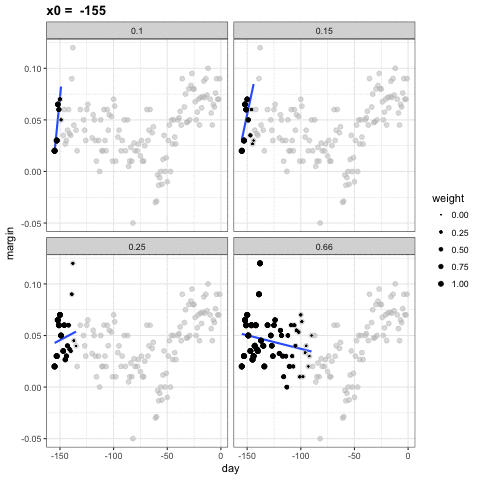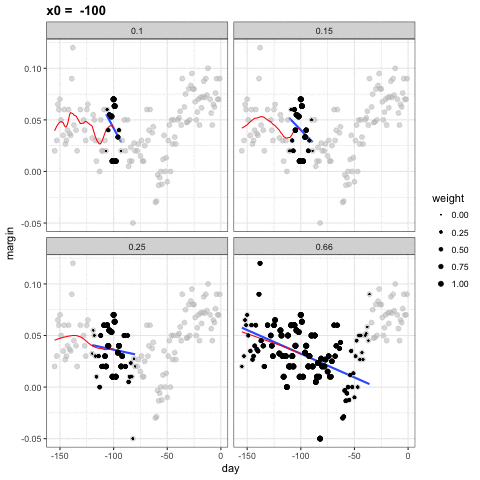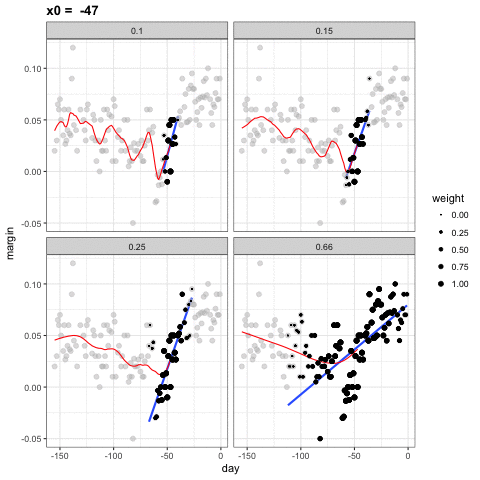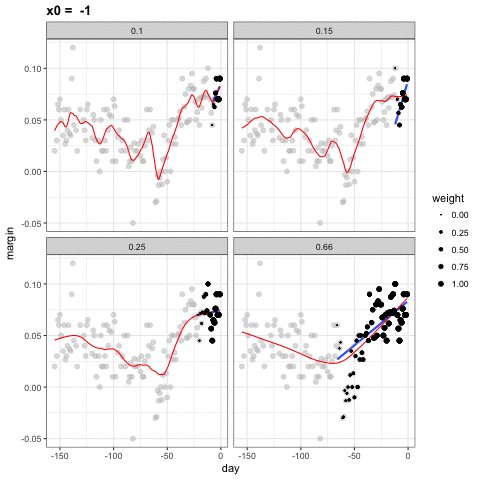
Aquí están los estimadores finales:

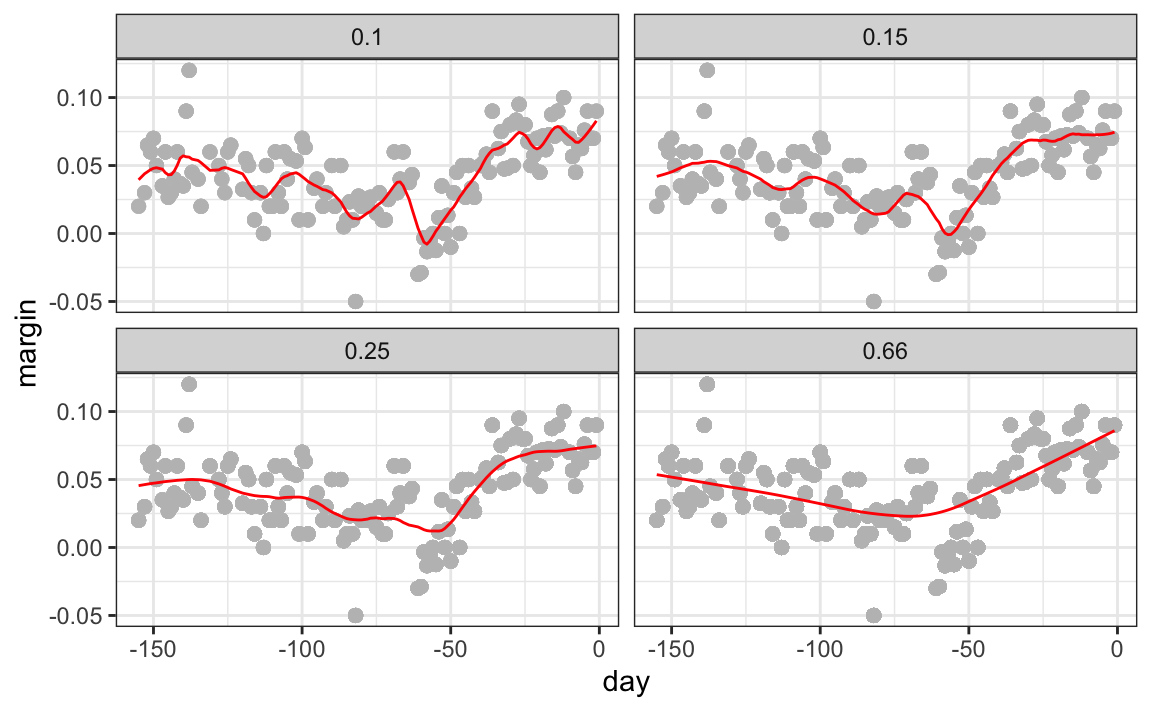
Hay otras tres diferencias entre loess y el típico suavizador de compartimiento.

1. En vez de mantener el tamaño del compartimiento igual, loess mantiene el mismo número de puntos utilizados en el ajuste local. Este número se controla a través del argumento span, que espera una proporción. Por ejemplo, si N es el número de puntos de datos y span=0.5, entonces para un determinado \(x\), loess usará los 0.5 * N puntos más cercanos a \(x\) para el ajuste.

2. Al ajustar una línea localmente, loess utiliza un enfoque ponderado. Básicamente, en lugar de usar mínimos cuadrados, minimizamos una versión ponderada:

\[ \sum_{i=1}^N w_0(x_i) \left[Y_i - \left\{\beta_0 + \beta_1 (x_i-x_0)\right\}\right]^2 \]

Sin embargo, en lugar del kernel gaussiano, loess usa una función llamada el Tukey tri-weight:

\[ W(u)= \left( 1 - |u|^3\right)^3 \mbox{ if } |u| \leq 1 \mbox{ and } W(u) = 0 \mbox{ if } |u| > 1 \]

Para definir los pesos, denotamos \(2h\) como el tamaño de la ventana y definimos:

\[ w_0(x_i) = W\left(\frac{x_i - x_0}{h}\right) \]

Este kernel difiere del kernel gaussiano en que más puntos obtienen valores más cercanos al máximo:

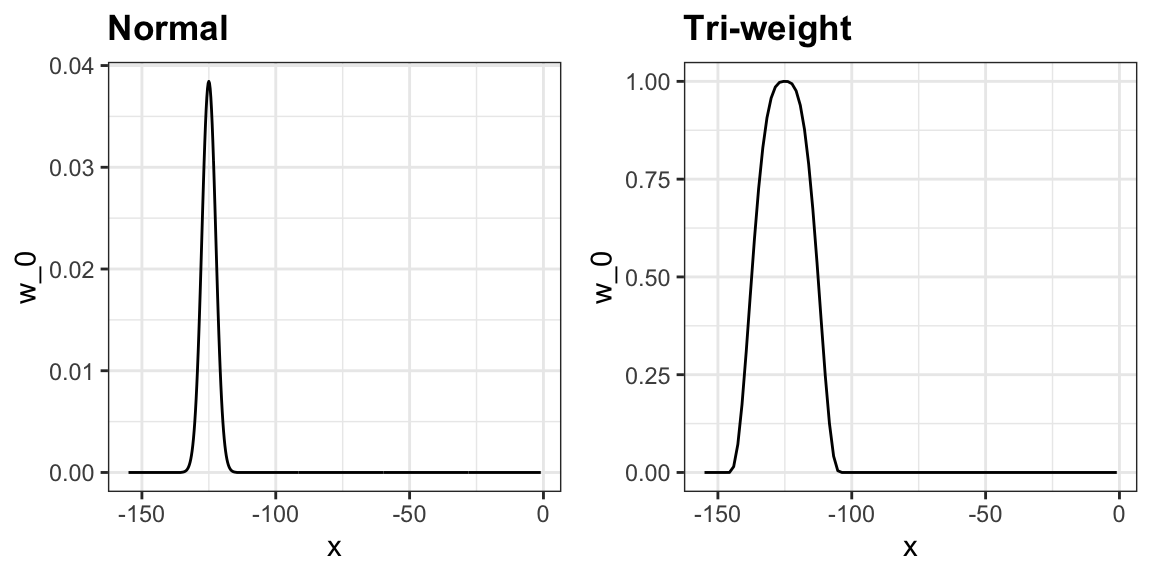
3. loess tiene la opción de ajustar el modelo local robustamente. Se implementa un algoritmo iterativo en el que, después de ajustar un modelo en una iteración, se detectan valores atípicos y se ponderan hacia abajo para la siguiente iteración. Para usar esta opción, usamos el argumento family="symmetric".

28.3.1 Ajustando con parábolas

El teorema de Taylor también nos dice que si miramos cualquier función matemática lo suficientemente cerca, parece una parábola. El teorema además establece que no tienen que mirar tan de cerca cuando se aproxima con parábolas como cuando se aproxima con líneas. Esto significa que podemos hacer que nuestras ventanas sean aún más grandes y ajustar parábolas en lugar de líneas.

\[ E[Y_i | X_i = x_i ] = \beta_0 + \beta_1 (x_i-x_0) + \beta_2 (x_i-x_0)^2 \mbox{ if } |x_i - x_0| \leq h \]

Este es el procedimiento por defecto de la función loess. Es posible que hayan notado que cuando mostramos el código para usar loess, configuramos degree = 1. Esto le dice a loess que se ajuste a polinomios de grado 1, un nombre elegante para líneas. Si leen la página de ayuda para loess, verán que, para el argumento degree, el valor predeterminado es 2. Por defecto, loess se ajusta a parábolas, no a líneas. Aquí hay una comparación de las líneas de ajuste (guiones rojos) y las parábolas de ajuste (naranja sólido):

total_days <- diff(range(polls_2008$day))
span <- 28/total_days
fit_1 <- loess(margin ~ day, degree=1, span = span, data=polls_2008)

fit_2 <- loess(margin ~ day, span = span, data=polls_2008)


polls_2008 |> mutate(smooth_1 = fit_1$fitted, smooth_2 = fit_2$fitted) |>
  ggplot(aes(day, margin)) +
  geom_point(size = 3, alpha = .5, color = "grey") +
  geom_line(aes(day, smooth_1), color="red", lty = 2) +
  geom_line(aes(day, smooth_2), color="orange", lty = 1)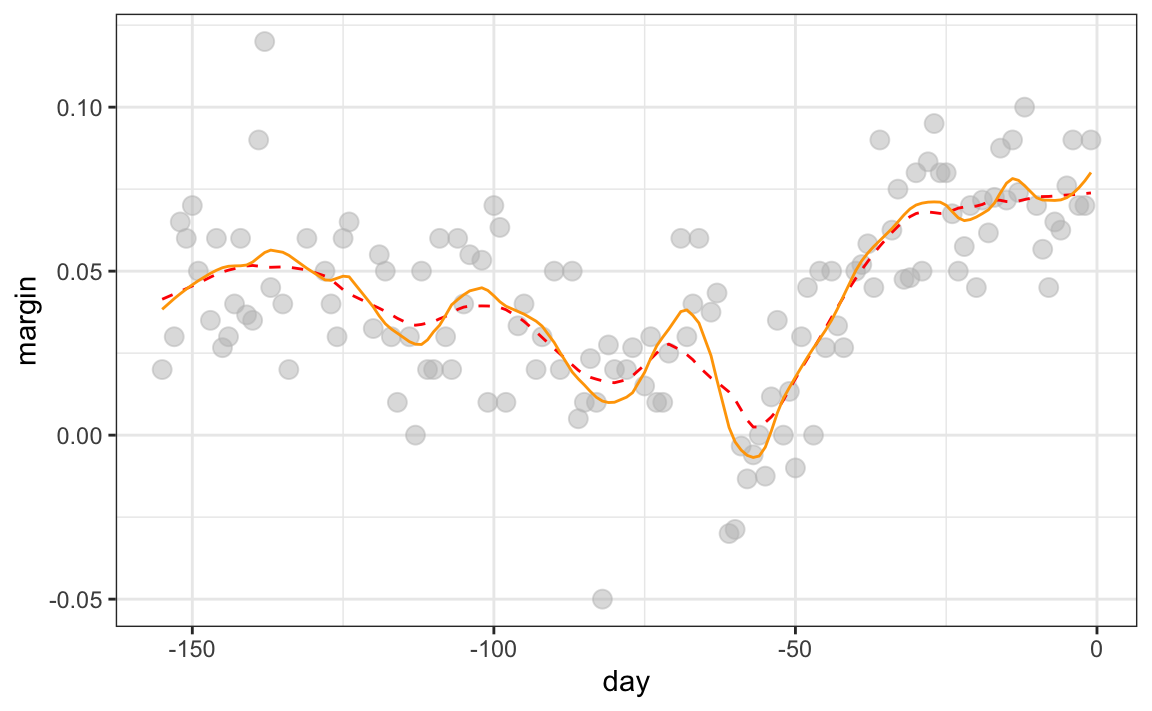

degree = 2 nos da resultados más ondulantes. Por eso, preferimos degree = 1 ya que es menos propenso a este tipo de ruido.

28.3.2 Cuidado con los parámetros de suavización predeterminados

ggplot2 utiliza loess en su función geom_smooth:

polls_2008 |> ggplot(aes(day, margin)) +
  geom_point() +
  geom_smooth()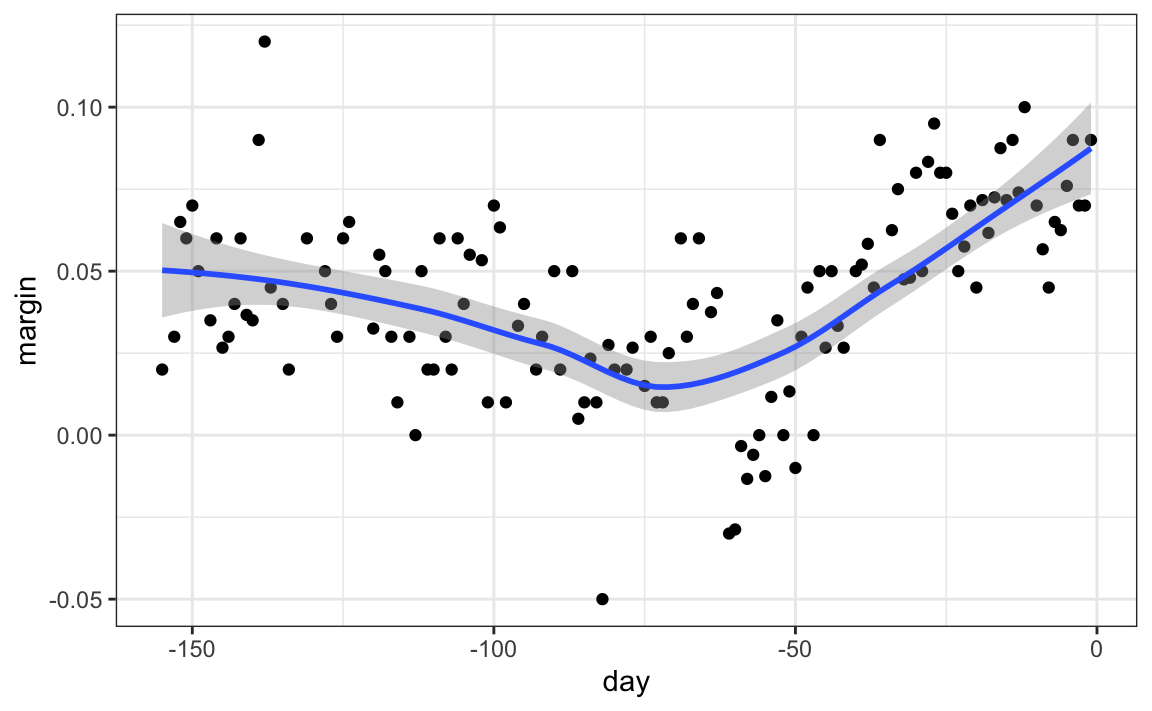

Pero tengan cuidado con los parámetros predeterminados ya que rara vez son óptimos. Afortunadamente, pueden cambiarlos fácilmente:

polls_2008 |> ggplot(aes(day, margin)) +
  geom_point() +
  geom_smooth(method = "loess", span = 0.15, method.args = list(degree=1))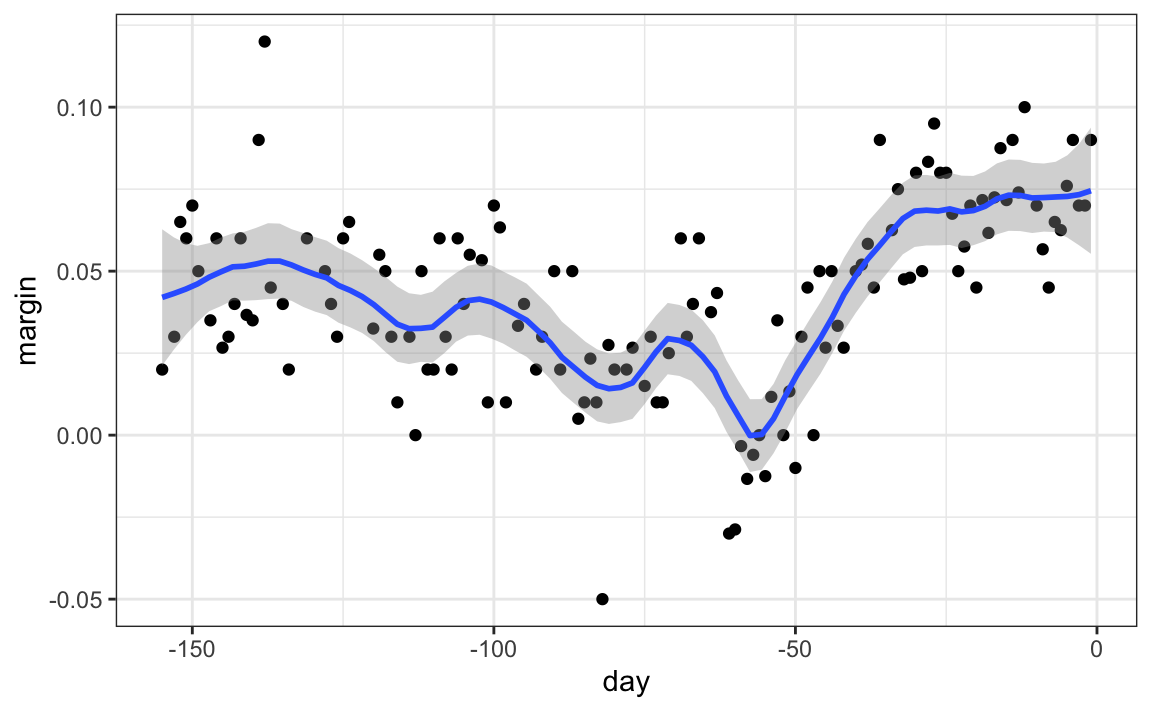

28.4 Conectando la suavización al machine learning

Para ver cómo la suavización se relaciona con el machine learning usando un ejemplo concreto, consideren nuestro ejemplo introducido en la Sección 27.8. Si definimos el resultado \(Y = 1\) para dígitos que son siete e \(Y=0\) para dígitos que son 2, entonces estamos interesados en estimar la probabilidad condicional:

\[ p(x_1, x_2) = \mbox{Pr}(Y=1 \mid X_1=x_1 , X_2 = x_2). \] con \(X_1\) y \(X_2\) los dos predictores definidos en la Sección 27.8. En este ejemplo, los 0s y 1s que observamos son “ruidosos” porque para algunas regiones las probabilidades \(p(x_1, x_2)\) no están tan cerca de 0 o 1. Por lo tanto, necesitamos estimar \(p(x_1, x_2)\). La suavización es una alternativa para lograr esto. En la Sección 27.8, vimos que la regresión lineal no era lo suficientemente flexible como para capturar la naturaleza no lineal de \(p(x_1, x_2)\); los enfoques de suavización, por ende, pueden proveer una mejora. En el siguiente capítulo, describimos un algoritmo popular de machine learning, k vecinos más cercanos, que se basa en la suavización por compartimientos.

28.5 Ejercicios

1. En la parte de wrangling de este libro, utilizamos el siguiente código para obtener recuentos de mortalidad para Puerto Rico para 2015-2018.

library(tidyverse)
library(lubridate)
library(purrr)
library(pdftools)
library(dslabs)

fn <- system.file("extdata", "RD-Mortality-Report_2015-18-180531.pdf",
                  package="dslabs")
dat <- map_df(str_split(pdf_text(fn), "\n"), function(s){
  s <- str_trim(s)
  header_index <- str_which(s, "2015")[1]
  tmp <- str_split(s[header_index], "\\s+", simplify = TRUE)
  month <- tmp[1]
  header <- tmp[-1]
  tail_index  <- str_which(s, "Total")
  n <- str_count(s, "\\d+")
  out <- c(1:header_index, which(n == 1), 
           which(n >= 28), tail_index:length(s))
  s[-out] |>  str_remove_all("[^\\d\\s]") |> str_trim() |>
    str_split_fixed("\\s+", n = 6) |> .[,1:5] |> as_tibble() |> 
    setNames(c("day", header)) |>
    mutate(month = month, day = as.numeric(day)) |>
    pivot_longer(-c(day, month), names_to = "year", values_to = "deaths") |>
    mutate(deaths = as.numeric(deaths))
}) |>
  mutate(month = recode(month, 
                        "JAN" = 1, "FEB" = 2, "MAR" = 3, 
                        "APR" = 4, "MAY" = 5, "JUN" = 6, 
                        "JUL" = 7, "AGO" = 8, "SEP" = 9, 
                        "OCT" = 10, "NOV" = 11, "DEC" = 12)) |>
  mutate(date = make_date(year, month, day)) |>
  filter(date <= "2018-05-01")

Utilice la función loess para obtener un estimador uniforme del número esperado de muertes como función de la fecha. Grafique la función suave que resulta. Use un span de dos meses.

2. Grafique los estimadores suaves como función del día del año, todas en el mismo gráfico pero con diferentes colores.

3. Suponga que queremos predecir 2s y 7s en nuestro set de datos mnist_27 con solo la segunda covariable. ¿Podemos hacer esto? A primera vista parece que los datos no tienen mucho poder predictivo. De hecho, si ajustamos una regresión logística regular, ¡el coeficiente para x_2 no es significativo!

library(broom)
library(dslabs)
data("mnist_27")
mnist_27$train |>
  glm(y ~ x_2, family = "binomial", data = _) |>
  tidy()

Graficar un diagrama de dispersión aquí no es útil ya que y es binario:

qplot(x_2, y, data = mnist_27$train)

Ajuste una línea loess a los datos anteriores y grafique los resultados. Observe que hay poder predictivo, excepto que la probabilidad condicional no es lineal.

---

107. https://www.flickr.com/photos/49707497@N06/7361631644↩︎

108. https://www.flickr.com/photos/number10gov/↩︎

109. https://creativecommons.org/licenses/by/2.0/↩︎